爱德思(Edexcel)物理U4复习笔记&简答题最全整理：进阶力学、电场、磁场和粒子

Carkree2025-11-19

本文共有两个部分，第一个部分是所有内容的复习笔记，第二个部分是所有简答题的历年答题模版。第一个部分的笔记很简练，更像是一个复习提纲，它不涉及复杂概念的辨析，也不涉及具体习题，但包括了所有的公式以及所有的知识点。第二个部分的简答题模板是我手动从历年的真题里整理的。

网上也有很多关于这方面的资料，这些内容主要是用于我的个人整理。Alevel物理的计算部分的难度比高考物理简单10倍，比较难的是简答题，毕竟有的时候对于计算题来说，就算你没完全理解知识点，也可以套公式得几分，但简答题就不一样了。长话短说，我认为学习物理的重中之重是理解知识点，理解每个概念都是怎么来的，在脑中不断演算，睡觉脑子也想着发电机模型。但是无论怎么讲，虽说它很简单，但是它的分数线一点也不低，A*是最多扣9分，A是最多扣19分，不知不觉中分就没了

开源，也是我的追求，让知识共享，让所有人共同享用。

第一部分：复习笔记

一、Momentum and Collision

Formula of momentum：$ p = mv $
Conservation of momentum的条件：In a closed system.
- 弹性碰撞（elastic collision）：动能守恒、动量守恒
- 非弹性碰撞（inelastic collision）：动量守恒、动能不守恒
Relative velocity:同向相减，异向相加
- 推导依据：
  1. 动量守恒：$ m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2 $ ①
  2. 动能守恒：$ \frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 $ ②
- 推导结果：$ u_1 - u_2 = v_2 - v_1 $
两个质量相同物体的弹性碰撞
- 由 $ u_A + u_B = v_A + v_B $ 和 $ u_A - u_B = v_B - v_A $，可得 $ u_A = v_B $，$ u_B = v_A $，即速度互换

二、Impulse

Formula：$ I = Ft $
$Change \ in \ momentum = \Delta p = p_{末} - p_{初} = mv - mu $
核心关系：力是动量的变化率（Force is the rate of change of momentum） $$F = \frac{m \Delta v}{t}$$
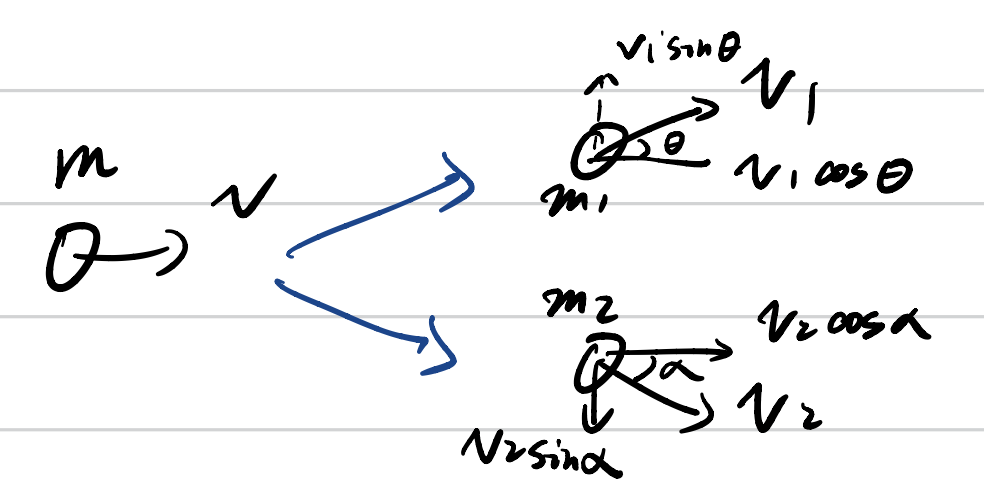
二维动量守恒（Conservation of momentum in 2D）
- 水平方向：$ m_1v_1\cos\theta + m_2v_2\cos\alpha = (m_1 + m_2)v\cos x $
- 竖直方向：$ m_1v_1\sin\theta = m_2v_2\sin\alpha $
- 总质量：$ m_{total} = m_1 + m_2 $
动量同动能的转换
因为$ p = mv $ ，所以$ v = \frac{p}{m} $
所以，$ E_k = \frac{1}{2}mv^2 = \frac{p^2}{2m} $

三、圆周运动（Circular Motion）

Linear velocity：$ v = \frac{s}{t} $
Angular velocity：$ \omega = \frac{\theta}{t} $（rad/s）
线速度与角速度关系：$ v = \omega r $
Period：转一圈的时间：$ T = \frac{2\pi}{\omega} $
Frequency：$ f = \frac{1}{T}$
Centripetal Force的formulae：
$$ F = ma = m\frac{v^2}{r} = m\omega^2 r = m\frac{4 {\pi}^2}{T^2} r = m4 {\pi}^2 f^2 r$$
竖直圆周运动（通过最高点和最低点）
- 通过最高点条件：$ N_2 + mg = m\frac{v^2}{r} $，需满足 $ N_2 \geq 0 $，即 $ v \geq \sqrt{gr} $
- 最低点：$ N_1 - mg = m\frac{v^2}{r} $
重要：推导centripetal acceleration的公式：使用vector

四、Electric Field

Charge：
1. Unit：库仑，标量
2. 基本电荷：$ e = 1.6 \times 10^{-19} \ C $
3. 规律：Like charges repel，different charges attract
Coulomb’s Law
1. 公式：$ F = k\frac{Q_1Q_2}{r^2} $（k = 8.99×10⁹ N·m²/C²，Q不带符号，r为电荷间距）
2. 力的方向：沿两电荷的圆心连线
Electric filed’s definition：A region where force will exert on the charged particle
Electric Field Strength：
1. Definition：Force per unit charge
2. Formulae：
  - $ E = \frac{F}{q} $
  - 仅适用点电荷电场： $ E = k\frac{Q}{r^2} $（Q为中心电荷）
- Unit：N/C，矢量
Electric Field Lines：
1. 电荷量越大，电场线越密集
2. 越靠近电荷，电场线越密集
3. 电场线越密集，场强越大
带电粒子在电场中的受力：
- 正电荷受力方向与电场方向相同
- 匀强电场（Uniform Electric Field）：大小和方向处处相同，
  - 匀强电场场强公式： $ E = \frac{V}{d} $（V为电势差，d为沿电场方向距离）
加速电场（Accelerating Electric Field）
- 电场力做功全部转化为动能：$ Fd = qV = qEd = \frac{1}{2}mv^2 $
Electric Potential Energy, EPE：
1. Definition：将电荷从无穷远移到某点所做的功
2. Formula：$ EPE = k\frac{Q_1Q_2}{r} $（带符号，这里是需要注意的，上面库仑定律是不带符号的，易错）
Electric Potential：
1. Definition：EPE per unit charge
2. Unit：J/C（伏特V）
3. Formulae：$ \phi = \frac{EPE}{q} = k\frac{Q}{r} $（Q为中心电荷，带符号）
4. 规律：沿电场线方向电势降低
密立根油滴实验
1. 在空气中达到终端速度（terminal velocity）
2. 平衡关系：$ mg = Eq = \frac{V}{d}q $

五、电容（Capacitance）与电容器（Capacitor）

电容的定义：Charge contained per unit potential difference
电容的公式：$ C = \frac{Q}{V} $
1. Unit：法拉（Farad, F）
2. 决定因素：由介电常数（ε₀）、极板面积（A）、极板间距（d）决定，与Q、V无关（$ C = \varepsilon_0\frac{A}{d} $）
电容器充放电原理
- 充电时：两极板带等量异号电荷，电路中有瞬时电流
- 充电条件：两极板间形成电势差，总电荷量不变
- 内部电场：匀强电场
电容器储存的能量：$ E = \frac{1}{2}QV = \frac{1}{2}CV^2 = \frac{Q^2}{2C} $
电容的串并联:
- In Series
  - 总电压：$ V_T = V_1 + V_2 $
  - 总电荷量：$ Q_T = Q_1 = Q_2 $
  - 总电容：$ \frac{1}{C_T} = \frac{1}{C_1} + \frac{1}{C_2} $
- In Parallel
  - 总电压：$ V_T = V_1 = V_2 $
  - 总电荷量：$ Q_T = Q_1 + Q_2 $
  - 总电容：$ C_T = C_1 + C_2 $
充放电过程（重要公式）
- 充电过程：
  1. 所有的物理量变化过程：
    $Q \uparrow ，C = \frac{Q \uparrow}{V \uparrow}，$
    一开始：$V_R = V_{电}$ ，后来 $V_R + V_C = V_{电}，$
    所以,$ V_C \uparrow 、V_R \downarrow ，I \downarrow = \frac{V_R \downarrow}{R}$
  2. 电压变化公式推导:
    $V_R = IR$
    $V_R = I_0 R \cdot e^{-\frac{t}{RC}} $
    $V_R = V_0 \cdot e^{-\frac{t}{RC}}$
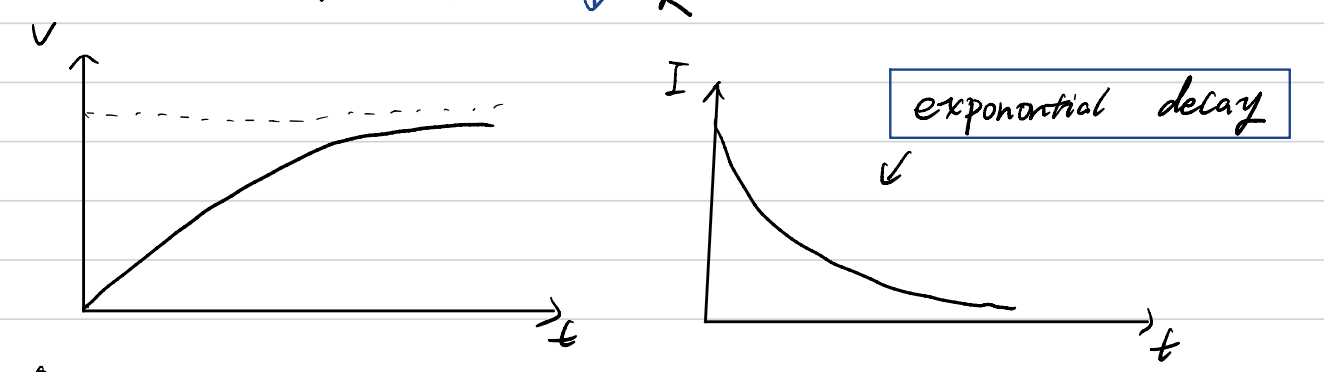
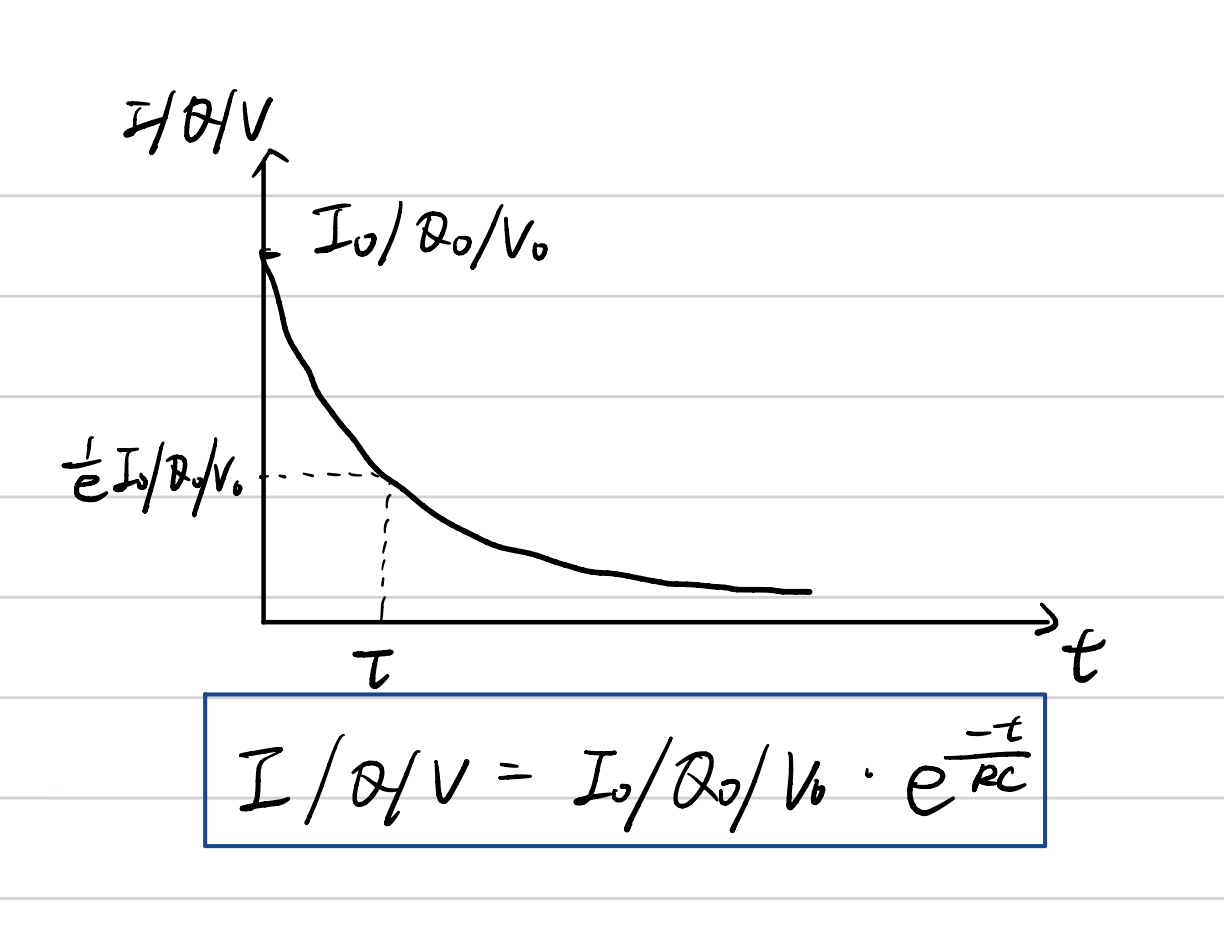
    $V_C = V_0 - V_0 \cdot e^{-\frac{t}{RC}}$（$V_R$：电阻两端电压，$V_C$：电容器两端电压）
  3. 电流变化：$ I = I_0e^{-\frac{t}{RC}} $，电流呈现exponential decay（图中拼写错误），特征很明显
- 放电过程：
  1. 所有的物理量变化过程：
    $Q \downarrow ，\overline{C} = \frac{Q \downarrow}{V \downarrow}，$
    $V_R \downarrow = V_C \downarrow ，$
    $I_R \downarrow = \frac{V_R \downarrow}{R}$
  2. 电压变化：$ V_C = V_0e^{-\frac{t}{RC}} $
  3. 电流变化：$ I = -I_0e^{-\frac{t}{RC}} $
    在放电过程中，所有的图像都是decay的，而充电过程中只有电流在decay，这个很好记忆。
- 时间常数 Time Constant：$ \tau = RC $，指的是当电容器的电流或者电压为原来的$\frac{1}{e}$的时候所花费的时间，如上图所示
  - 遇到电容的大计算题，绝对和time constant有关系，就直接无脑往time constant上靠，基本过程是：通过 $ \ln(I/V/Q) - t $ 图像斜率计算 $ \tau $，进而求R或C

六、磁场（Magnetic Field）

定义：对磁性物体或运动电荷施加力的区域（A region where force will act on magnetic objects or moving charged particles）
磁场方向：N极受力方向即为磁场方向，磁场线为闭合曲线
Magnetic Flux Density, B:
- 表示磁场的强弱，单位：特斯拉（T）
Magnetic Flux, $Φ$：
- 公式：$ \Phi = BA\cos\theta $（θ为磁场与平面夹角，垂直时$ \Phi = BA $）
- 单位：韦伯（Wb）
- 磁通量变化：线圈翻转180°时，$ \Delta\Phi = 2BA $
Magnetic Flux Linkage）：$ N\Phi = NBA $（N为线圈匝数）
磁场与电流的方向表示
- ⊗：垂直纸面向外
- ⊙：垂直纸面向里
磁场中的力
1. 一个通电导线在磁场中受到安培力的作用，力的方向使用左手定则判断，力的大小为$F = BIL$，且必须B和I垂直才有力
2. 一个粒子在磁场中受到洛伦兹力的作用，力的方向和速度方向垂直，力的大小为$F = Bqv$
左手定则：
1. 在alevel中，左手定则为Fleming Left Hand Rule，用于判断通电导线在磁场中本身受到的力。三个指头分别为$FBI$，具体不在此阐述
2. 在中国普通高中，左手定则为：将磁感线穿过左手手掌，四指方向则为电流方向，大拇指为在磁场中受到的力的方向。

七、电磁感应（Electromagnetic Induction）

感应电流产生条件：闭合电路的部分导体切割磁感线，或磁通量发生变化
法拉第电磁感应定律（Faraday’s Law）
- 内容：感应电动势大小与磁通量变化率成正比
- 公式：$ \varepsilon = -N\frac{\Delta\Phi}{\Delta t} $（N为匝数，负号表示阻碍变化）
右手定则：
1. 同上，Fleming Right Hand Rule，用于判断感应电流的方向，三个指头分别为$FBI$，具体不在此阐述
2. 在中国普通高中，右手定则为：磁感线穿过右手手掌，拇指为外力方向
楞次定律（Lenz’s Law）
- 内容：感应电流的方向总是阻止感应电流产生
如上图所示，上下两块磁铁构成磁场，在其间放置一个闭合回路的导线（不通电）。这时若施加一个大小为$F$的外力使其切割磁感线，则会产生感应电动势和感应电流，感应电流的方向使用右手定则判断，感应电动势的大小使用$emf = \frac{d\phi}{dt}$计算。与此同时，根据楞次定律，会产生一个和导线运动方向相反的力，也就是图示的大小为$f$的力，这个力的大小可以用安培力的计算公式来计算。
通电螺线管
- 通电螺线圈本身会产生磁场，磁场的方向用右手螺旋定则判断，大拇指为N极方向。
- 若将以磁铁靠近通电螺线管，此时会有斥力；当磁铁原理时，会有吸引力；这被称作“来拒去留”。
- 若在通电螺线圈外面再绕上一层闭合环路导线，并将通电螺线圈的电源换成交流电电源（a.c. supply），则会出现一个变换的磁场，进而有magnetic flux linkage的变化，导致闭合环路导线产生感应电动势和感应电流
发电机（Generator）与电动机（Motor）
- 发电机：无外接电源，通过线圈切割磁感线产生感应电流（电磁感应原理）
- 电动机：有外接电源，通电线圈在磁场中受力转动（安培力原理）
右手定则和左手定则的易混点：

左手定则用来判断通电导线在磁场中本身受到的力，左手定则中的F是通电导线本身受到的力。左手定则还可以用来判断磁场的方向。
右手定则用来判断感应电流的方向，右手定则中的F的方向时人施加外力的方向

磁场这部分是U4中最难的，也是比较爱出计算和简答题的部分。

八、原子结构与粒子物理（Probing Matter）

（一）原子模型（Atomic Models）

粒子
- 质子（Proton）：带正电，$ +1.6 \times 10^{-19} \ C $
- 中子（Neutron）：不带电
- 电子（Electron）：带负电，$ -1.6 \times 10^{-19} \ C $
  - proton = electron = 原子序数
- 离子（Ion）：电荷转移形成，正离子（失去电子），负离子（得到电子）
  
  重点单词：
  atom 原子
  nucleus 原子核
  nucleons 核子（中子+质子）
  neutron 中子
  proton 质子
α粒子散射实验（Alpha Particle Scattering Experiment）
1. 现象：The majority of alpha-particles went straight through the gold foil without deflection
  
  结论：The atom is a mainly empty space
2. 现象：Some alpha-particles deflected through small angle of <$10^{\circ}$
  
  结论：Atoms having a concentration of charge in a central nucleus
3. 现象：Only a small number of alpha-particles straight back at angle of >$90^{\circ}$
  
  结论：Nucleus is extremely small and there is concentration of mass in the center of the atom. And nucleus contain almost all the mass
模型发展：Pudding Model →Rutherford Model（通过alpha粒子实验推翻了pudding model）

（二）热电子发射（Thermionic Emission）

电子激发方式：加热（热能量使电子逸出）、光照（光子与电子相互作用）、电子碰撞（能量传递）

其中，电路1因生热，导致elctron被释放

电路2形成电场，导致electron被加速。这是很重要的部分，当题目告知列式时，要能够找到正确的电压。

（三）带电粒子在电磁场中的运动

这些公式完全不用背，只需要理解公式是什么意思，物理就是找量，列式

电场加速：$ qV = \frac{1}{2}mv^2 $ （能量守恒列式） → $ v = \sqrt{\frac{2qV}{m}} $
磁场中圆周运动：$ qvB = m\frac{v^2}{r} $ （圆周运动公式） → 轨道半径$ r = \frac{mv}{qB} = \frac{p}{qB} $
周期：$ T = \frac{2\pi m}{qB} $（与速度无关）

（四）加速器（Accelerators）

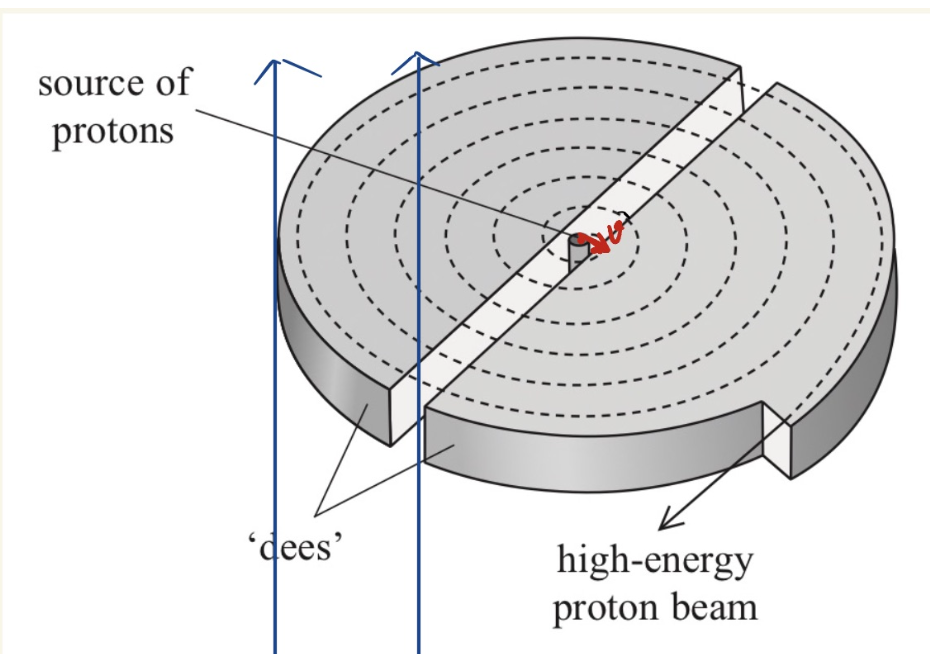
回旋加速器（Cyclotron）
- 原理：粒子在电场中（两个dees之间）加速，在磁场中（两个dees内）做匀速圆周运动。连接交流电电源，电场方向会变化。
线性加速器（Linac）
- 原理：
  1. 圆桶内部无电场，粒子匀速运动
  2. 圆桶之间有电场，粒子加速运动
  3. 交流电源频率与粒子在圆桶内运动时间匹配，圆桶长度逐渐增加

（五）基本作用力与粒子分类

基本作用力（Fundamental Forces）
- Gravitational Force：$ F = G\frac{m_1m_2}{r^2} $
- Electromagnetic Interaction）：$ F = k\frac{Q_1Q_2}{r^2} $
- 强核力（Strong Nuclear Force）：维系原子核稳定，作用于强子之间
粒子分类
- Hadron：由夸克组成
  - Baryon：3个夸克
  - Meson：1个夸克 + 1个反夸克
- Lepton：一个基本粒子（基本粒子即最小的单位，不可再分）

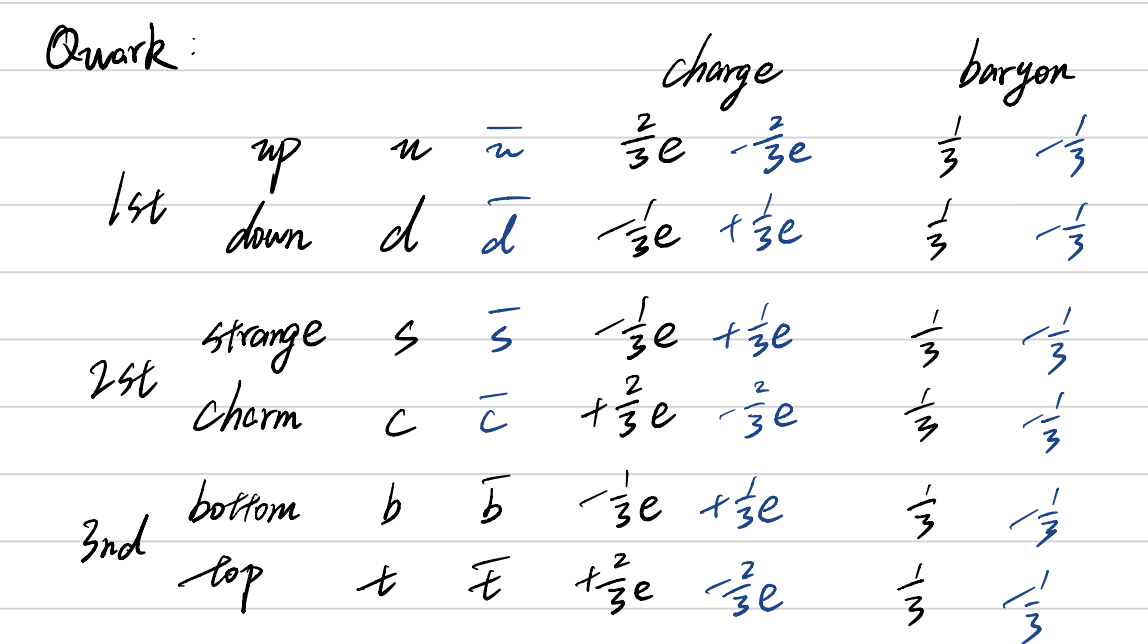
夸克（Quark）
- 夸克是基本粒子，是宇宙中一切可见物质的基本组成部份，不可再分。（毛泽东同志曾指出：物质是无限可分的，让我们拭目以待？）
- 反夸克（Anti-quark）：质量相同，电性相反
Lepton的类型：

反物质（Antimatter）与湮灭（Annihilation）
- 反物质：与普通物质粒子质量相同、电性相反。正常物质由若干个电子组成，反物质由若干个正电子（positron，电量为+1）组成（2025年10月考试真题）
- 湮灭：粒子与反粒子碰撞后消失，质量转化为能量（γ射线），遵循质能方程$ E = mc^2 $
气泡室(Bubble chamber)：
1. 带电粒子会在气泡室内留下轨迹
2. 质量越大，电离能力越强，留下的轨迹越深
3. 由于碰撞和摩擦，curvature（曲率）减小
4. $r = \frac{mv}{qB}$，速度大或质量大，轨道半径极大，近似直线轨迹
5. 例：探究neutron的结构：
  - 证明neutron不带电：像气泡室发射中子，无轨迹产生
  - 证明虽然neutron不带电，但仍然有电子分布：用电子撞击neutron，出现了不同的轨迹（不同轨迹代表带不同的电量）

（六）Decay

β⁺衰变：$ p^+ \rightarrow n^0 + e^+ + \nu_e $（质子→中子+正电子+中微子）
同位素（Isotope）：质子数相同，中子数不同的原子

（七）相对论

Rest Energy：$ E = mc^2 $
时间膨胀（Time Dilation）：运动物体的时间变慢，$ \tau = \tau_0\sqrt{1 - \frac{v^2}{c^2}} $（$ \tau_0 $为固有时间）（不考公式）。将粒子从山上扔下，速度变快，它的life time会变长。

（十）用电子探究neutron的结构

中子不带电（neutral）：气泡室中发射中子，无轨迹产生
电荷分布：用电子轰击中子，产生不同轨迹，证明中子电荷分布不均匀

单位前缀（Prefixes）

前缀	符号	倍数
Tera	T	10¹²
Giga	G	10⁹
Mega	M	10⁶
Kilo	k	10³
milli	m	10⁻³
micro	µ	10⁻⁶
nano	n	10⁻⁹
pico	p	10⁻¹²

第二部分：简答题整理

为什么极少的粒子在gold foil被deflect超过90度可以证明atoms having a concentration of charge in a central nucleus

Alpha particle need large force to deflect them through angles greater than $90^{\circ}$
Few were close enough so the space occupied must be very small

Linac如何加速粒子/为什么tube最终变得一样长

Adjacent drift tubes have opposite charge
There is an electric filed between drift tubes.
This exerts a force on particles, particles accelerate in the gaps.
While the particles are traveling through a particular drift tube, because frequency of a.c. supply is constant, so the polarity reverses.
Time taken for the particles to travel between adjacent tubes is constant
s = vt, particles travel further in a fixed time with a higher speed
The particles approach the speed of light. Speed become constant so distance travelled in a fixed amount of time become constant.

为什么electron能用来探究原子核的结构？

能被加速到很大的速度
电子波长和atomic nuclei的大小差不多
电子可以衍射
不是因为电子带负电

alpha粒子实验的结论

The majority of alpha-particles went straight through the gold foil without deflection

The atom is a mainly empty space
Some alpha-particles deflected through small angle of <$10^{\circ}$

Atoms having a concentration of charge in a central nucleus
Only a small number of alpha-particles straight back at angle of >$90^{\circ}$

Nucleus is extremely small and there is concentration of mass in the center of the atom. And nucleus contain almost all the mass

为什么gold foil要很薄

Alpha particles are strongly ionising.
So alpha particles can only penetrate a thin sheet.

JJ Thomson model of atom是什么内容

The atom is believed to have an equally distributed mass throughout.

为什么alpha粒子比其他更适合去做实验

Beta particles more penetrating.
So beta particles less likely to deflect.
Gamma particles isn’t charged.
So gamma particles will not experience any electrostatic force.

描述衰变是否可以产生

Conservation of charge, xx = xx
Conservation of baryon number, xx = xx
Conservation of lepton number, xx = xx
Combination all of above, the decay obeys three conservation laws.

为什么要对着高能量撞击产生质量大的粒子/怎么样的撞击可以产生一个质量大的粒子

$E = m c^2$
Total momentum before collision is zero, so it have low momentum after collision
They do not have hight KE
Almost all energy available for formation of particles
Need a large amount of energy to create a high-mass particle.

金属导体的电流是如何产生的

Magnetic field
Cut magnetic filed lines
induced emf
complete circuit, induced current

气泡室为什么能捕捉到带电粒子的踪迹

The particle is ionising
A track is formed by the ionised particles produced.

如何证明是中性的

没有track
conservation of charge

为什么移动的粒子有了一个更长的mean lifetime

Close to speed of light
Relativistic effect on particle lifetime

描述thermionic emission是如何创造electron beam的

The thermionic emission emit electrons.
The electric field is used to accelerate them.

Electron beam持续运动为什么会减少直径和强度

Electron collisions decrease momentum of electrons, reducing radius ($r = \frac{p}{Bq}$)
Electrons absorbed by helium so intensity decreases.